Implementing Heap in TypeScript

Priority Queue is an extension of queue with following properties:

• Every item has a priority associated with it.
• An element with high priority is dequeued before an element with low priority.
• If two elements have the same priority, they are served according to their order in the queue.

A typical priority queue supports following operations:

• insert(item, priority): Inserts an item with given priority.
• getHighestPriority(): Returns the highest priority item.
• deleteHighestPriority(): Removes the highest priority item.

Applications of Priority Queue:

• CPU Scheduling
• Graph algorithms like Dijkstra’s shortest path algorithm, Prim’s Minimum Spanning Tree, etc
• All queue applications where priority is involved.
• Data Compression (Huffman codes)
• Find the largest M items in a stream of N items.

Ways to implement Priority Queue:

• Arrays - Insertion and Deletion is expensive in order to maintain the priority.
• LinkedList -> Same as array, but deletion is fast.
• Binary Heap -> Best

Binary Heap (Min Heap or Max Heap)

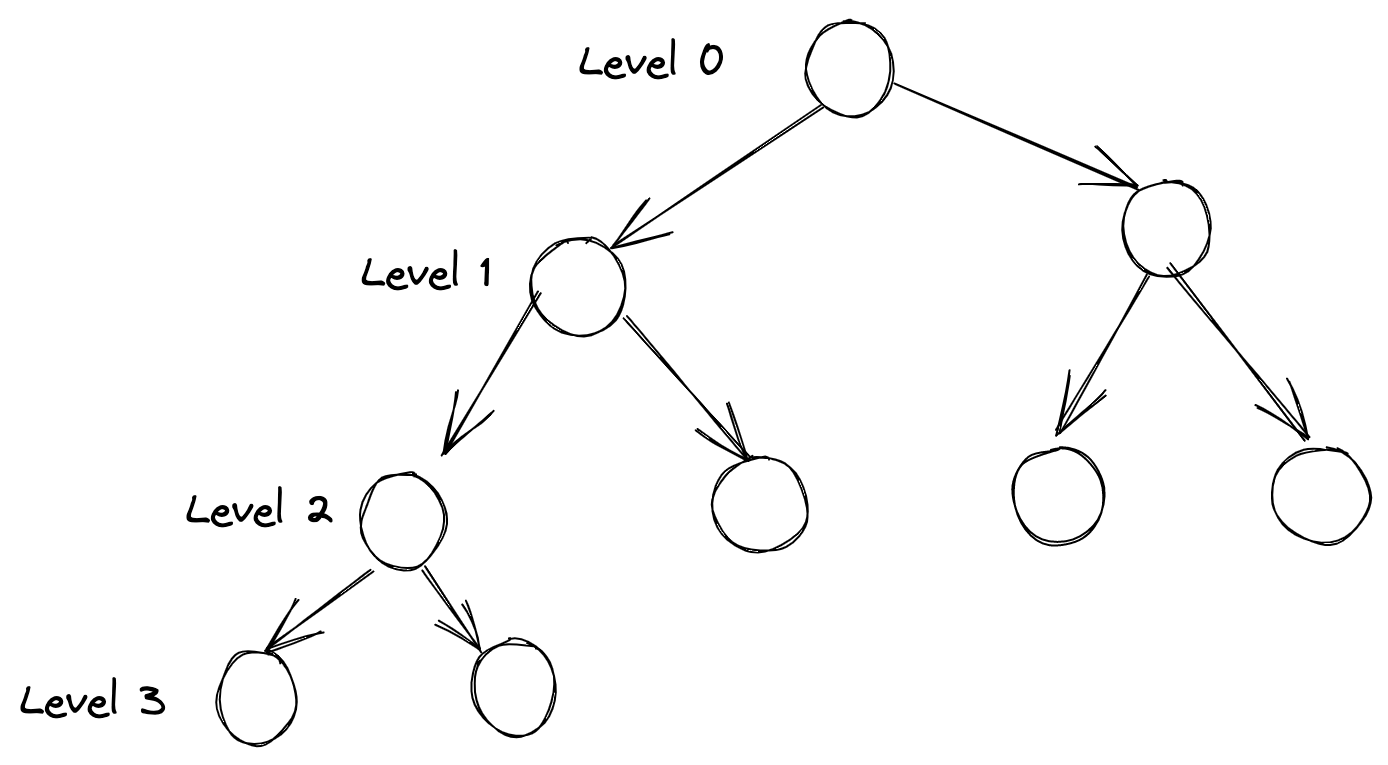
• Based on the idea = 10 of Complete Binary Tree.
• Binary Tree: Empty or Nodes to left and right binary tree.
• Complete Binary Tree: Perfectly Balanced, except for the bottom level and the bottom level has all keys as left as possible.
  • Perfectly Balanced, except for Level 3
  • Height of a Complete Binary Tree of N node is Log N. In the shown tree, there are 9 nodes ==> Log 9 = Log 3^2 = 2 Log 3. (3 Levels)

Implementation: Array representation of the heap ordered complete binary tree.

Heap Ordered Binary Tree:

• Keys in nodes.
• Parent's key is greater than children's keys. This is important.

Properties of Binary Heap:

• Largest key is arr[1], which is the root of the binary tree.
• Parent of node at 'k' index is at k/2 index. (It's integer divide. No floats)
• Children of a node 'k' are at index '2k' and '2k + 1', given we start indexing from 1 instead of 0.

Consider this array:

index       0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
arr[index] [_, T, S, R, P, N, O, A, E, I,  H, G]

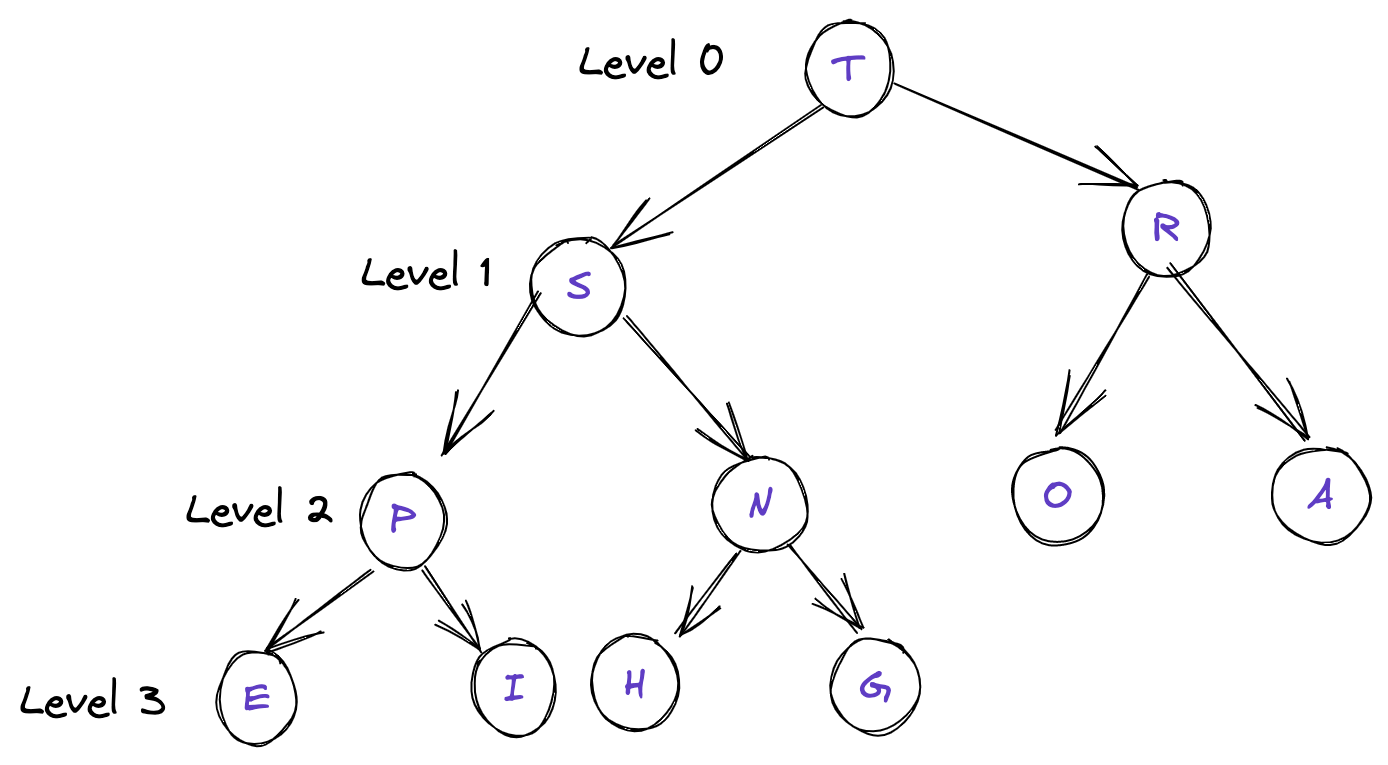
What's the parent of H & G?

Parent of node at 'k' is at k/2. Here k = 10(H), so parent will be at 10/2 = 5. Element at index 5 is N, which is correct!
So, we don't need actual tree to represent these data structures. Array indices are sufficient.

Time complexity for building a Binary Heap is O(N). Read more about the complexity here

Implementation

type Comparator<T> = (a: T, b: T) => number

class Heap<T> {
  items: T[]
  comparator: Comparator<T>

  constructor(list: T[], comparator: Comparator<T>) {
    this.items = list || []
    this.comparator = comparator
    this.buildHeap()
  }

  buildHeap(): void {
    for (let i = Math.floor(this.size() / 2) - 1; i >= 0; i--) {
      this.moveDown(i)
    }
  }

  moveDown(curIdx: number): void {
    const lastIndex = this.size() - 1
    const items = this.items
    while (this.leftChild(curIdx) <= lastIndex) {
      let i = this.leftChild(curIdx)

      // if i is not the last element -> compare i with i+1
      // if i was the last element, i+1 would give us index out of bound!
      if (i < lastIndex && this.comparator(items[i], items[i + 1]) < 0) {
        i++
      }

      if (this.comparator(items[i], items[curIdx]) < 0) {
        break
      }

      this.exchange(curIdx, i)
      curIdx = i
    }
  }

  moveUp(curIdx: number): void {
    while (curIdx > 0) {
      let parent = this.parent(curIdx)
      if (this.comparator(this.items[curIdx], this.items[parent]) < 0) break
      this.exchange(parent, curIdx)
      curIdx = parent
    }
  }

  offer(value: T) {
    this.items.push(value)
    this.moveUp(this.size() - 1)
  }

  poll(): T | null {
    if (this.size() === 0) return null

    const item = this.items[0]
    const last = this.items.pop()

    if (this.size() && last) {
      this.items[0] = last
      this.moveDown(0)
    }

    return item
  }

  leftChild(parent: number): number {
    return 2 * parent + 1
  }

  rightChild(parent: number): number {
    return 2 * parent + 2
  }

  parent(child: number): number {
    return Math.floor((child - 1) / 2)
  }

  peek(): T {
    return this.items[0]
  }

  size(): number {
    return this.items.length
  }

  isEmpty(): boolean {
    return this.size() === 0
  }

  exchange(i: number, j: number): void {
    let temp = this.items[i]
    this.items[i] = this.items[j]
    this.items[j] = temp
  }
}